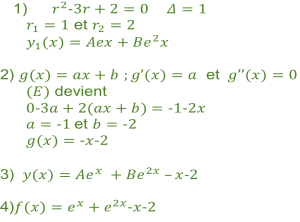QUESTION 18
On considère l’équation différentielle
(E): Y’’ – 3y’ + 2y = -1 – 2x
1)- Déterminer les solutions de l’équation différentielle
(E1) : Y’’ – 3y’ + 2y = 0
Déterminer les constantes réelles a et b pour que la fonction g définie sur IR par g(x) = ax + b. Soit une solution particulière de l’équation (E).
2)- En déduire l’ensemble des solutions de l’équation différentielle (E)
3)- Déterminer la solution f de l’équation(E)
4)- Déterminer la solution f de l’équation(E) qui vérifie les conditions initiales : f(0) = 0 et f'(0) = 2