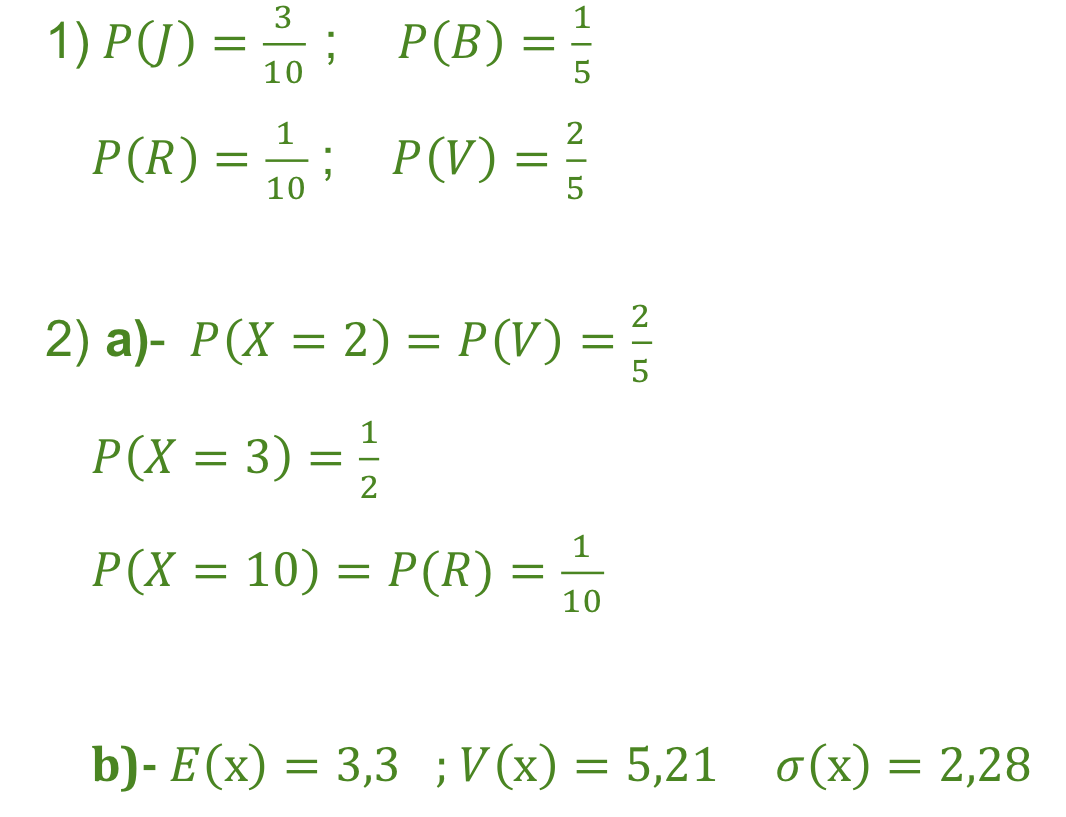QUESTION 18
On considère une urne contenant 3 boules jaunes, 2 bleues, 1 rouge et 4 vertes toutes indiscernables au toucher. On tire au hasard une boule de l’urne.
Calculer la probabilité des évènements suivants :
J= « tirer une boule jaune»
B= « tirer une boule bleue»
R= « tirer une boule rouge»
V= « tirer une boule verte»
En fonction de la couleur tirée, on se voit attribuer une somme d’argent selon la règle suivante :
-Rouge, on gagne 10F
-Verte, on gagne 2F
-Jaune ou bleue, on gagne 3F
Soit X la variable aléatoire qui associe à chaque tirage le gain réalisé
Déduire de la question 1 les valeurs de P(X=2) ; P(X=3) et P(X=10)
Calculer l’espérance mathématique de X, sa variation et son écart-type.